Utilization of Intelligent Tutoring System (ITS) in mathematics learning

Tsai Chen, Aida MdYunus, Wan Zah Wan Ali, AbRahim Bakar
Universiti Putra Malaysia, Malaysia

ABSTRACT

Intelligent Tutoring Systems (ITS) represents some of the knowledge and reasoning of good one-to-one human tutors, and consequently are able to coach students in a more detailed way as compared to the Computer Assisted Instructions (CAI) packages.Canfield (2001) defines ITS as a system that is able to diagnose and adapt to student's knowledge and skills.  According to Canfield, ITS is able to provide precise feedbacks when mistakes are made and able to present new topics when the student is ready to learn.  ITS is part of a new breed of instructional computer programs. This paper discusses the benefits of using an ITS as complement to the use CAI materials such as the courseware in promoting the learning of mathematics.  Benefits of using an ITS have been proven in aspects such as generating useful feedbacks to students in learning mathematic, assisting learning of higher order subject matter and cultivating higher order skills, offering a learning environment that motivates learners, giving useful instant feedback to learners, and providing positive effects on student’s achievement.

Keywords: Intelligent Tutoring System; Computer Assisted Instruction; Technology in Mathematics Education; Information Communication Technology in Education; Tools in Mathematics Learning

INTRODUCTION

Information Communication Technology (ICT) is widely used in business, education, management and various other fields.  To provide a more effective learning environment, Computer Assisted Instruction (CAI) had been developed.  Since its introduction by Patrick Suppes at Stanford University during the 1960s, it has evolved as a learning tool that provides text and multiple-choice questions or problems to students, offers immediate feedback, notes incorrect responses, summarizes students' performance, and generates exercises for worksheets and tests. CAI typically presents tasks for which there is only one correct answer, it can evaluate simple numeric or very simple alphabetic responses, but it cannot evaluate complex student responses. Basically CAI programs tutor and drill students, diagnose problems, keep records of student progress and present material to students. Since its early years, CAI has expanded its influence into all subject areas (Piccoli, Ahmad & Ives 2001).  Numerous studies (Alexender 1999, Jain & Getis 2003, Leung 2003) had been conducted to compare the effectiveness of CAI to conventional method of instruction.  These researches revealed statistical differences on students’ achievement and attitude between CAI group and the conventional group.

Previous studies such as Bangert-Drowns, Kulik and Kulik (1985), Owens and Waxman (1994), Teh and Fraser (1995), Yalcinalp, Geban and Ozkan (1995) and Leung (2003) conclusively showed that CAI has led to improvement in students’ achievement.  Students in the CAI group were able to perform significantly better than students in the control group.  However, studies such as Glickman and Dixon (2002), have indicated that Intelligent Tutoring System (ITS) as a delivery system have a greater potential than CAI to help students overcome difficulties in solving mathematics problems. 

According to Ester (1994), while CAI may be somewhat effective in helping learners, they do not provide the same kind of personalised attention that a student would receive from a human tutor.  In recent years, research on the use of ICT in mathematics learning had focused on the integration of Artificial Intelligence (AI) elements in CAI packages for learning. Patterson (1990) defined Artificial Intelligence (AI) as a branch of computer science concerned with the study and creation of computer systems that exhibit some form of intelligence. He further stated that AI is a system that can learn new concepts and tasks.  It is a system that can understand a natural language and able to perform other types of feats that require human types of intelligence. Ester asserts that AI is able to prepare a more human based interactive learning environment for students.  Human based interactive learning environment is important in learning because it involves students in active learning. 

Heffernan (2001) asserts that as the techniques of AI becomes widely known and appreciated in the field of educational computing, AI with interests in education has also undergone changes in direction.  He also stressed that the overall aim of developing AI is to enable the computer to be effective and act as a knowledgeable agent in the teaching and learning process.  A major stand of research has been the design of the so-called Intelligent Tutoring Systems (ITS) which require knowledge representations to provide models of the subject domain, the learner capabilities and the tutorial pedagogy (Heffernan 2001).

According to Cumming and Abbott (1988), ITS such as PROLOG by Robert Kowalski have been under development for nearly twenty years.  Other expert systems, such as SNOOPY (Schauer & Staringer 1988) have already been used in western schools since twenty years ago.  SNOOPY is a simple system to demonstrate some of the methods and techniques of artificial intelligence.  It is essentially a dialogue program with simple natural language understanding capabilities.

Recent works on ITS such as Wayang Outpost developed by Arroyo et al. (2004) tutors students for the mathematics section of the Scholastic Aptitude Test (SAT). It has several distinctive features; help with multimedia animations and sound, problems embedded in narrative and fantasy contexts, alternative teaching strategies for students of different mental rotation abilities and memory retrieval speeds. Evaluations that Arroyo et al. (2004) conducted proved that students learn with the tutor, but learning depends on the interaction of teaching strategies and cognitive abilities.

The objective of an ITS is to provide a teaching process that adapts to the students’ needs by exploring and understanding the student’s special needs and interests (Kaplan & Rock 1995).  Research in the field of ITS has always had a strong focus on the development of comprehensive student models, based on the assumption that within a problem solving context, learner’s thinking processes can be modelled, traced, and corrected using computers (Siemer-Matravers 1999).

According to McArthur, Lewis, and Bishay (1994), ITS attempts to capture a method of teaching and learning exemplified by a one-to-one human tutoring interaction.  One-to-one tutoring allows learning to be highly individualized and consistently yields better outcomes than other methods of teaching.  Unlike previous CAI systems, ITS represents some of the knowledge and reasoning of good one-to-one human tutors, and consequently can coach in a much more detailed way than CAI systems.

INTELLIGENT TUTORING SYSTEM (ITS)

Canfield (2001) defines intelligent tutoring system (ITS) as a system that is able to diagnose and adapt to student's knowledge and skills.  According to Canfield (2001), ITS is able to provide precise feedbacks when mistakes are made and able to present new topics when the student is ready to learn.  Intelligent tutoring systems are part of a new breed of instructional computer programs.

ITS which adapts a one-to-one tutoring approach, has aspired to generate highly detailed feedback on problem solving to learners.  It provides a more integrated approach, with the inclusion of exploratory activities to help promote the development of real life mathematics.  On the other hand, CAI packages are designed to provide information or demonstrations of procedures and require students to practice in a reinforced environment where the sequence is determined by the system.   The main strength in ITS is its ability to provide immediate feedback on students’ work. ITS does not just provide feedback such as correct or wrong answer for the student’s mathematics solution but it also provides details of the misconception that the student face.  Educators such as Duchastel (1988) believe that a dialogue-based ITS provides an interactive dialog with students which is similar to the role of human tutor in helping students to learn.

The ITS discussed in this paper, Ms. Lindquist developed by Heffernan (2001), provides learning episodes based on dialog-based interactions with student. It is able to diagnose the learner’s action in order to infer the learner’s cognitive state, such as his or her level of knowledge or proficiency. 

A general model of Intelligent Tutoring Systems includes three basic modules: domain knowledge, student model, and tutorial model. Using the domain knowledge, ITS should be able to solve problems regarding the pedagogical module which is given to the students. The Tutorial Model controls the interaction with the student based on its own knowledge of teaching.  In short, the architecture of an ITS system (Figure 1) consists of four major parts particularly, Domain Knowledge System, Student Model, Tutorial Model and Integration Model (Kearlsley 1987).

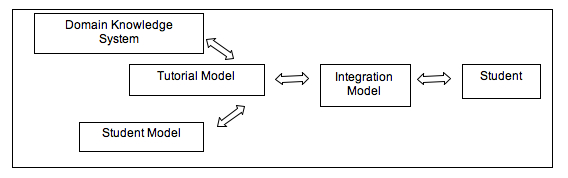
Figure 1:  The architecture of an ITS system

The Domain Knowledge System contains information about all the related knowledge in the specified course.  It stores all the theory and database related to the course.  It can be labelled as the library of the system.  It generates new problems based on the student’s response. This system accumulates and provides knowledge on subject domain, maintains testing exercises, provides these data to its users and other agents, and analyses the students "feedback" in domain terms.

The Domain Knowledge System does work well without the Tutorial Model.  According to Duchastel (1986), the Tutorial Model contains information about effective tutorial practices and monitors the status of the Student Model. It recommends appropriate dialogue between the ITS and the student.  Both the Tutorial Model and the Student Model ‘cooperate’ with eachother to work effectively.  Tutorial Model controls the learning process, applies different educational strategies according to the cognitive and essential personal features of the student, together with his/her educational progress.  Kearlsley (1987) further explained that the function of the Tutorial Model is meant to imitate the process in which a human tutor would engage in similar circumstances.  It includes a set of tutorial rules that will redirect the learning interaction. From the data in the Student Model, the Tutorial Model will generate which tutorial strategy is to be used in the next step of instruction.  The architecture of Ms. Lindquist is illustrated in Figure 2.

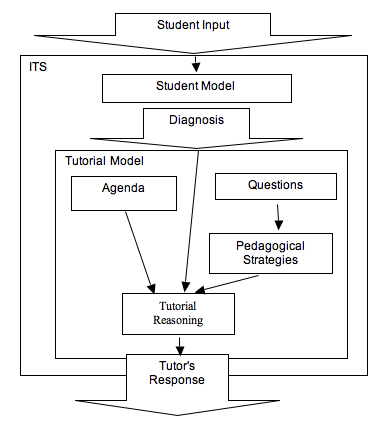
Figure 2:  The architecture of Ms. Lindquist system

The Tutorial Model of Ms. Lindquist was designed to conduct a rational dialog, which entails being able to have sub-dialogs that ask new questions rather then simply giving hints to students.  In the process of learning, it recognizes correct answers given by the student and gives positive feedback on those portions.  While the Tutorial Model plans on how to correct the incorrect answer, it also supports multi-step tutorial strategies and provides feedback to the user.  To ensure students gain an effective learning experience, the Tutorial Model gives reflective follow-up questions, particularly upon gaining evidence of weak understanding by the students. 

Heffernan and Koedinger (2002) stated that the term Student Model refers to a cognitive or expert model.  Student Model stores information regarding student’s knowledge on particular skills.  Kearlsley (1987) pointed out that the Student Model contains information about the student’s knowledge and their experience throughout the learning process with ITS.   Most of the student model in ITS was constructed by comparing the student’s performance with the computer-based expert behaviour on the same task.  Based on the comparison, the ITS system will determine student’s mastery level in the specified learning context.

In Ms. Lindquist, Student Model does the diagnosing (Figure 2).  It is similar to the traditional Student Model in other ITS.  However, it is more human-like in carrying on a running conversation, complete with feedbacks and follow-up questions.  Further clarification was made by Heffernan and Koedinger (2002) by stating the following:

We do not want a computer system that cannot understand a student if she gives an answer that has parts that are completely correct and parts that are wrong. We want the system to be able to understand as much as possible of what a student says and be able to give positive feedback even when the overall answer to a question might be incorrect. (p.3)

Hence, the Student Model plays an important role in assessing student’s knowledge and makes a hypothesis on the conceptions and reasoning strategies employed by the student to achieve his/her current knowledge state.  Kearsley (1987) listed four major information sources for maintaining the Student Model; i) student’s problem-solving behaviour as observed by the system; ii) direct questions posed by the student; iii) assumptions based on the student’s learning experience and iv) assumptions based on some measures of the difficulty of the subject matter material.

Diagnosis of the Student Model is used as an input for the Tutorial Model.  It is always presented in two methods, Socratic method and coaching method.  The Socratic Method provides students with questions guiding them through the process of understanding and correcting their misconceptions.  While the coaching method provides students with an environment in which to engage in activities, in order to learn related skills and general problem-solving skills (Heffernan & Koedinger 2002). The illustration in Figure 3 displays the guidance provided by an ITS system.

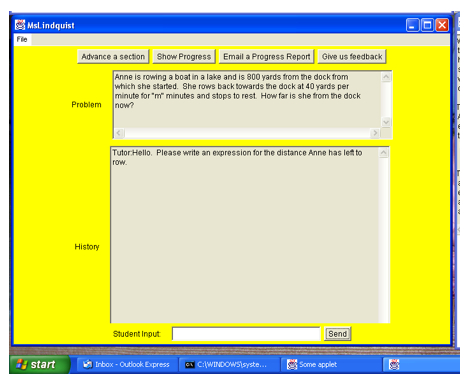
Figure 3: Tutorial session of Ms. Lindquist

The Integration System controls the entire process. It asks the students questions and it passes the student’s response to the other systems.  Hence the student’s response was evaluated by comparing the Student Model with the domain knowledge to determine flaws in the student’s response.  Based on this evaluation, the Domain System generates a new problem, which is then presented to the student in the manner suggested by the Tutorial Model.

Ms. Lindquist, the free algebra tutor for mathematical word problems can be downloaded from the internet (Figure 4).  The development was funded by the National Science Foundation and the Spencer Foundation. Developed by Neil Heffernan, the program is named after Ms. Cristina Lindquist who was the expert human tutor video taped. The latest Ms. Lindquist program can be viewed at http://www.AlgebraTutor.org/.

Figure 4: Ms Lindquist website

According to Heffernan (2001), Ms. Lindquist has five levels of problems; (i) one-operator problems, (ii) one-operator problems involving distance, rate and time, (iii) two-operator problems involving linear forms, (iv) two-operator problems involving division and parenthesis, and (v) three and four operator problems.  After the student selects the level he wishes to work on, the student is presented with a problem to symbolize an algebraic expression for a given quantity expressed as an English phrase.  The student will get promoted to the next section if he/she answers correctly the next row of questions.  The following diagram shows the screen that informs the user of the number of trials and the number of questions answered correctly.

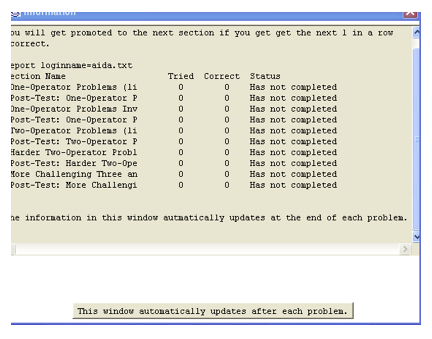
Figure 5: Display of number of trials and number of questions answered correctly in Ms. Lindquist

Heffernan (2001) further elaborated that Ms. Lindquist uses a simple mastery criterion.  Students must acquire a certain number of correct answers to pass through a level and to proceed to a new question. In Ms. Lindquist, the number of problems that the student needs to answer correctly is three, four or five questions, depending on the context.  Ms. Lindquist engages the students in a dialogue that tries to encourage the student to solve the mathematics problem although the student does not answer the problem correctly at first.  A new problem will only be given once the student solves the previous problem.  Once a level is completed, the student will then move forward to the next level.

Ms. Lindquist uses five different tutorial strategies; i) Concrete Articulation; ii) Explain in English first; iii) Introduce Variable; iv) Convert the problem into an example to explain, and v) Cut to the chase.  The first strategy requires students to work on a concrete example, which will make it easier for them to understand and thus able to write the full algebraic expression.  For example, if the answer for a mathematics solution is "800-40/x", where the “x” is an unknown algebraic symbol, the system will guide the student to solve the "40/x" part by providing a concrete example, and this is followed by the sub-goal involving the subtraction.  Students will be given step by step guides to achieve the sub-goal, which then leads them in solving the whole problem.

The second strategy is the ‘Explain in English first’ strategy.  This strategy is based on the idea that students are more familiar with expressing ideas in English than using algebraic expressions.  Thus, this strategy will first guide students to achieve the goal in applying explanation in English and thus step-by-step, translating the mathematical problem into algebraic expressions.  Figure 6 illustrates the different windows in Ms. Lindquist system.

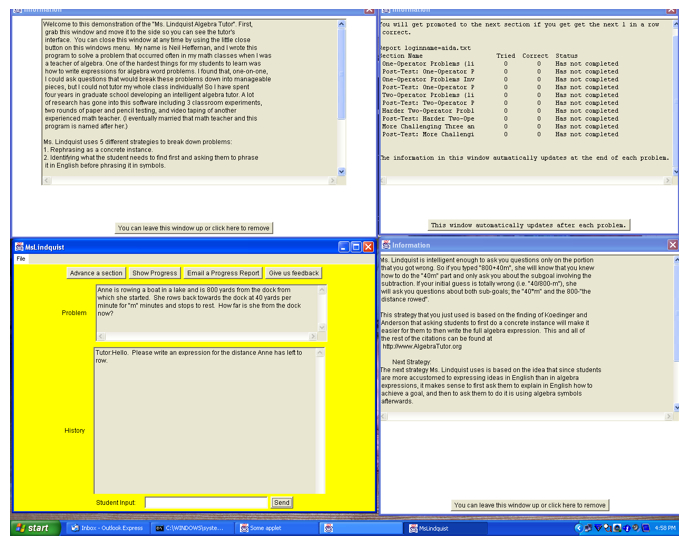
Figure 6: Different windows of Ms. Lindquist system

The next strategy is to introduce the variable.  Ms. Lindquist will give an example to explain the strategy employed, thus providing scaffolding to students by introducing a variable.  Students improve on their ability to write expressions for word problems by practicing these sorts of problems.  For example, when the system provide a task whose solution is “7s +10a”, students will be guided to write out the “x + y” from the task first. Hence, Ms. Lindquist will use scaffolding strategy to guide student to get the “7s” and “10a”.  Finally the student will get the solution for the problem as “7s +10a”.

The fourth strategy used in Ms. Lindquist is conversion of problems into examples.  This strategy is based on the premise that students learn well when presented with complete examples.  Therefore, this strategy guides students to translate problems from words to symbols.  Students will also be guided to translate symbols into word problems.  Heffernan (2001) believed that getting practice in translating words to symbols and vice-versa is important in the learning of algebra. 

The last strategy that is included in Ms. Lindquist is the ‘Cut to the chase’. The system just gives the student the direct answer when the student is not able to solve the problems.  This is to ensure that the student will go on to the next problem and the program will try to guide the student again.  It is probably true that student do not learn as much on a problem if they are just given the answer.  However, the trade off is that students would be able to work on more problems in the limited amount of time as compared to the other strategies that Ms. Lindquist provide.

IMPACT OF ITS ON STUDENT ACHIEVEMENT

According to Sleeman and Brown (1982), past researches had focused on supportive learning environments in transforming factual knowledge into experiential knowledge.  They stated that ITS attempts to combine the problem-solving experience and the motivation to learn under the effective guidance of tutorial interaction.  Generating explanations to students in a friendly format is a very important element in the ITS environment.  Thus, researcher in ITS always intends to investigate the issues of generating useful feedbacks to students in learning mathematics (Callear 1999).   

In a meta-analysis study conducted by Yaakub and Finch (2001) to compare the effectiveness of Computer-Assisted Instruction (CAI) in technical education with ITS, the focus was on studies on use of CAI in guiding higher order learning.  The 21 studies selected yielded 28 effect sizes with an overall effect size coefficient of 0.35 for CAI-based technical education instruction.  Results revealed that ITS was significantly more effective than CAI.  This finding provides support on the benefits of using ITS in teaching higher order subject matter and higher order skills.

In evaluating the ITS called Whole-course Intelligent Tutoring System (WITS) (Callear 1999), six students from a local school and three adult students were selected as subjects of the study.  Interactions between the subject and the system were investigated.  Results of the study showed that all nine students found the feedback facility from the system very useful, and subjects found the profile interesting.  This result indicated that students appreciated the ongoing and detailed feedback from WITS. Callear (1999) concluded that ITS is able to offer a learning environment that motivates learners and gives useful instant feedback to learners.

In addition, Moundridou and Virvou (2002) in their evaluation of the ITS, Web-based Authoring tool for Algebra Related domains (WEAR), found positive result on the usage.  The participants in the experiment were forty eight college students from the University of Piraeus, Greece.  Twenty six of them were studying Informatics and the rest were studying Economics.  Those students were randomly divided into two equal-sized groups, the ‘Agent’ group and the ‘Non-Agent’ group.  The experiment started with a pre-test, consisting of five problems.  Students were asked to work on the pre-test using paper and pencil.  For each student, the time needed and the score achieved in the pre-test were recorded.  Both groups scored similarly in the pre-test and needed about the same time to complete it.  This was an indication that both groups were equally capable of dealing with the tasks they had to perform. Results from the study showed that both groups improved their time and scores in the post-test.  Based on this, it could be assumed that the tutoring system achieved its goal in improving student’s performance.

In the study by Ramachandran and Stottler (2003), they found no significant difference between the control group and experimental group on a Meta-Cognitive Computer-based Tutor for High-School Algebra.  The Algebra tutor was evaluated twice, but only over short periods of time.  On both these occasions, students worked with the tutor for about thirty minutes to two hours.  Due to the limited interaction, the researcher did not observe any significant improvements in problem-solving performance as a result of using the tutor.  On both surveys, students using the tutor expressed an overall positive reaction.  The study yield useful information for further enhancement to the tutor.

Koedinger, Anderson, Hadley and Mark (1997) in their study on application of ITS in learning mathematics reported positive effects on students’ achievement for the experimental group.  The population was students from three public high schools with similar demographics and students’ aptitudes.  Students in the experimental classes received two treatments, the new Pittsburgh Urban Mathematics Project (PUMP) curriculum and they worked with an ITS system called Practical Algebra Tutor (PAT). In their experiment, students worked on six lessons in a complete PAT environment and one self study lesson on the tutor module.  The "PUMP+PAT" group consisted of 20 algebra classes that involved 470 students and 10 teachers.  On the contrary, the control classes received traditional instruction and did not use PAT.  Researchers looked into students’ mathematic grades in the previous school year to verify that there were no differences in students’ prior mathematical background that would put the PUMP+PAT group at an advantage.  It was found that after the treatment period, students in the PUMP+PAT group scored significantly higher than the control group.  Thus the result showed that ITS is effective in helping students to learn mathematics.

Another research on the use ITS in the learning of mathematics was conducted by Abidin and Hartley (1998) who investigated the effectiveness of an ITS software, FunctionLab, using the pre-test and post-test experimental design.  The pre-test consisted of five questions that included problem solving questions.  Students were given the pre-test before they were involved in treatment that uses the FunctionLab as their learning tool.  The pre-test was followed by a FunctionLab training session for each subject.  For the first phase of the session, students were given introduction on the language used in FunctionLab. In the second phase of the study, a demonstration regarding operations of FunctionLab software was given to the students.  After 90 minutes of treatment, a post-test was administered on the group of students. Positive result was established in student’s problem solving skill.  This indicated that students were able to solve more mathematical problems in the post-test.

Nathan, Kintsch, and Young (1992) administered an experiment with the ITS system, ‘Animate’, that helped students to comprehend algebraic word problems.  The program was designed to help students in understanding the relationship between formal mathematical word problems and the situations described in the problems.  Students in the experimental group wrote a formal equation to solve the problem and animated the equation to see if it depicted the expected solution.  In this study, 46 undergraduate students from the University of Colorado participated in a two-hour experiment as part of their course requirements.  Subjects were randomly assigned to one of four treatment groups; three of the groups used ITS while one group was the traditional control group.  Results of the study showed that students from the ITS groups were more effective in their problem solving in algebra.  Those groups of students showed higher scores in the post-test. 

The Geometry Explanation Tutor developed by Aleven et al. (2004) was based on the hypothesis that natural language dialogue is a more effective way to support self-explanation.  The ITS helps students to state explanations of their problem-solving steps using their own words.  According to Aleven et al., one of the findings is that students who received higher-quality feedbacks from the system made greater progress in their dialogues and learned more, providing some measure of confidence that progress is a useful intermediate variable to guide further system development.  They also found that students who tended to reference-specific problem elements in their explanations, rather than stating a general problem-solving principle, had lower learning gains as compared to the other students.

In an experimental study, Tsai (2007) had compared the use of CAI followed by ITS (CAI+ITS) and use of CAI only in the learning of algebraic expression.  The result of the study showed that there was significant difference in students’ achievement in algebraic expression between students who learn with CAI+ITS and who learn with CAI only.  This finding provides supporting evidence for the benefits of using CAI+ITS in the learning of algebraic expression among students. 

Majority of the studies discussed had showed consistent results, favouring the use of ITS in the learning of Mathematics.  Benefits of using an ITS have been proven in aspects such as generating useful feedbacks to students in learning mathematic (Aleven et al. 2004, Callear 1999), assisting learning of higher order subject matter and cultivating higher order skills (Yaakub & Finch 2001), offering a learning environment that motivates learners and giving useful instant feedback to learners (Callear 1999), and providing positive effects on student’s achievement (Koedinger, Anderson, & Hadley 1997; Tsai 2007).

CONCLUSION

Various types of CAI packages are being used for teaching and learning in schools and in higher institutions.  CAI packages may assume the role as a tutor.  However, the involvement of users of CAI in the learning is rather passive.  Users click and move forward to the next screen, follow the instructions given and interaction is maintained at a minimal level.  The CAI program is not able to evaluate students’ answers and guide students in solving the given problem.

In the last eight years, numerous researches have shown the benefits of the ITS.  As stated by Wilkinson-Riddle and Patel (1998), ITS does not attempt to change the process of education in any radical way but it recognizes the strengths of a human teacher and helps remove some of the  teachers’ burden in teaching.  The advantage of the ITS is that it’s one-to-one tutoring function enables it to adapt tutoring strategies according to the needs of the individual student (Zhou 2000).  Since ITS has proved to be effective in guiding students’ learning, integration of ITS elements must be considered in the development of computer-based or multimedia learning programs.  Educators, policymakers, and educational media developers should study the comparative advantage of an ITS based learning tools as compared to CAI based learning tools.  Although this would certainly rocket the development price, decision on such investments must not be ignored since ITS could well serves as an intelligent partner to human cognition and helps students to become self-regulated learners. 

REFERENCES

Abidin, B. & Hartley, J. R.  1998. “Developing mathematical problem solving skills”. Journal of Computer Assisted Learning, vol 14, pp. 278-291.

Alexendar, M. 1999. “Interactive Computer Software in College Algebra”, Retrieved on Dec 20, 2005, from http://archives.math.utk.edu/ICTCM/EP-11/C1/pdf/paper.pdf elearnig-papr4

Aleven, V., Ogan, A., Popescu, O., Torrey, C. &  Koedinger, K. (2004).  Evaluating the Effectiveness of a Tutorial Dialogue System for Self-Explanation. Intelligent Tutoring Systems: Proceedings of the 7th International Conference, ITS 2004, Maceió, Alagoas, Brazil, August 30 - September 3, pp. 443-454.

Arroyo, I., Beal, C. Murray, T., Walles, R. & Woolf, B. P. (2004).  Web-based intelligent multimedia tutoring for high stakes achievement tests.  Intelligent Tutoring Systems: Proceedings of the 7th International Conference, ITS 2004, Maceió, Alagoas, Brazil, August 30 - September 3, pp. 468-477.

Bangert-Drowns, R., Kulik, J. & Kulik, C.  1985. “Effectiveness of computer-based education in secondary schools”. Journal of Computer-Based Instruction, vol. 12, pp. 59-68.

Callear, D. 1999. “Intelligent tutoring environments as teacher substitutes: Use and feasibility”. Educational Technology, vol. 39, no. 5, pp.6-8.

Canfield, W. 2001. “ALEKS: A Web-based intelligent tutoring system”. Mathematics and Computer Education, vol. 35, no. 2, pp.152-158.

Cumming, G. & Abbott, E. 1988. “PROLOG and expert systems for children’s learning”.  In P. Ercoli & R. Lewis (eds.), pp.163 – 175.  Proceeding of the IFIP TC3 Working Conference on Artificial Intelligence Tools in Education. Frascati, Italy.

Duchastel, P. 1988. Models for AI in education and training: Artificial Intelligence Tools in Education, Elsevier Science Publishers, North-Holland, Holland.

Ester, D. 1994. “CAI, lecture, and student learning style: The differential effects of instructional method”.   Journal of Research on Computing in Education, vol. 27. no. 2, pp. 129-140.

Glickman, C. &  Dixon, J. 2002. “Teaching intermediate algebra using reform computer assisted instruction”. The International Journal of Computer Algebra in Mathematics Education, vol. 9, no. 1, pp. 75-83.

Heffernan, N. 2001.  Intelligent tutoring systems have forgotten the tutor: Adding a cognitive model of an experienced human tutor.  Dissertation.  Computer Science Department, School of Computer Science, Carnegie Mellon University. Technical Report CMU-CS-01-127.

Heffernan, N. & Koedinger, K. 2002. “An intelligent tutoring system incorporating a model of an experienced human tutor”. In S. Cerri, G. Gouarderes, & F. Paraguacu (eds.), Proceedings of the 6th International Conference on Intelligent Tutoring Systems, pp. 596-608. Springer-Verlag, Berlin.

Jain, C. & Getis, A. 2003. “The effectiveness of internet-based instruction: An experiment in physical geography”. Journal of Geography in Higher Education, vol. 27, no. 2, pp. 153-167.

Kaplan, R. & Rock, D. 1995. “New directions for intelligent tutoring”.  AI Expert, vol. 10, no. 2, pp. 30-40.

Kearlsley, G. 1987. Artificial intelligence and instruction: Applications and methods, Addison-Wesley,Reading, MA.

Koedinger, K., Anderson, J., Hadley, W., & Mark, M.  1997.  “Intelligent tutoring goes to school in the big city”. International Journal of Artificial Intelligence in Education, vol. 8, pp. 30-43.

Leung, K. 2003. “Evaluating the effectiveness of e-learning”. Computer Science Education, vol. 13, no. 2, pp.123-136.

McArthur, D., Lewis, M., & Bishay, M. 1994. The role of artificial intelligence in education:  Current progress and future prospects, RAND Corporation, Santa Monica, CA.

Moundridou, M. & Virvou, M. 2002. “Evaluating the persona effect of an interface agent in tutoring system”. Journal of Computer Assisted Learning, vol.18, no. 3, pp. 253-261.

Nathan, M., Kintsch, W., & Young, E. 1992. “A theory of algebra word problem comprehension and its implications for the design of computer learning environments”. Cognition and Instruction, vol. 9, no. 4, pp. 329 – 389.

Owens, E. & Waxman, H. 1994. “Comparing the effectiveness of computer-assisted instruction and conventional instruction in mathematics for African-American postsecondary students”. International Journal of Instructional Media, vol. 21, no. 4, pp. 327-393.

Patterson, D. 1990. Introduction to Artificial Intelligence and Expert Systems, Prentice Hall, New Jersey.

Piccoli, G., Ahmad, R., & Ives, B. 2001. “Web-based virtual learning environment: A research framework and a preliminary assessment of effectiveness in basic IT skills training”. MIS Quarterly, vol. 25, no. 4, pp. 401-426.

Ramachandran, S. & Stottler, R. 2003. “A Meta-Cognitive Computer-based Tutor for High-School Algebra”. World Conference on Educational Multimedia, Hypermedia and Telecommunications, vol. 1, pp. 911- 914.

Schauer, H & Staringer, W. 1988. “SNOOPY: A little LOGO expert system”. In P. Ercoli & R. Lewis, Artificial Intelligence Tools in Education, pp. 177 -182. Proceeding of the IFIP TC3 Working Conference on Artificial Intelligence Tools in Education, Frascati, Italy.

Siemer-Matravers, J. 1999. Intelligent tutoring systems and learning as a social activity. Educational Technology, vol. 39, no. 5, pp. 29-32.

Sleeman, D., & Brown, J. 1982.  “Introduction: Intelligence Tutoring Systems”.  In D. Sleeman & J. Brown (eds), Intelligent Tutoring Systems, pp. 1-11,  Academic Press, New York.

Teh, G. & Fraser, B. 1995. “Gender differences in achievement and attitudes among students using computer-assisted instruction”. International Journal of Instructional Media, vol. 22, no. 2, pp. 111–120.

Tsai, C. 2007.  Effects of intelligent tutoring system on students’ achievement in algebraic expression.  Unpublished Masters thesis, Universiti Putra Malaysia, Serdang, Selangor.

Wilkinson-Riddle, G. & Patel, A. 1998. “Strategies for the creation, design and implementation of effective interactive computer-aided learning software in numerate business subjects-The Byzantium experience”. Information Services & Use, vol. 18, no.1-2, pp.127-135.

Yaakub, M. & Finch, C. 2001. Effectiveness of Computer-Assisted Instruction in Technical Education: A Meta- Analysis. In J. Kapes, (ed), Occupational Education Forum/Workforce Education Forum (OEF/WEF), vol. 28, no. 2, pp. 5-19.

Yalcinalp, S., Geban, O., & Ozkan, I. 1995. Effectiveness of Using Computer-Assisted Supplementary Instruction for teaching the mole concept. Journal of Research in Science Teaching, vol. 32, no.10, pp.1083-1095.   

Zhou, Y. 2000. Building a new student model to support adaptive tutoring in a natural language dialogue system. Unpublished doctoral dissertation, Illinois Institute of Technology.

Copyright for articles published in this journal is retained by the authors, with first publication rights granted to the journal. By virtue of their appearance in this open access journal, articles are free to use, with proper attribution, in educational and other non-commercial settings. Original article at: http://ijedict.dec.uwi.edu//viewarticle.php?id=594&layout=html